Inhoud
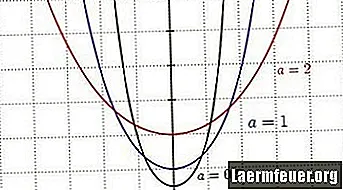
Een bovenleiding is de vorm die een kabel aanneemt wanneer deze wordt ondersteund door zijn uiteinden en alleen onder invloed van zijn gewicht wordt uitgeoefend. Het wordt veel gebruikt in de bouw, met name hangbruggen, en een omgekeerde bovenleiding wordt al sinds de oudheid gebruikt voor de constructie van bogen. De bovenleidingcurve is een hyperbolische cosinusfunctie die een "U" -vorm heeft die lijkt op een parabool. De vorm van een specifieke bovenleiding kan worden bepaald door de schaalfactor.
Berekening van de bovenleiding
Stap 1
Bereken de standaard bovenleidingfunctie y = a cosh (x / a), waarbij y de y van het cartesische vlak is, x de x van het cartesische vlak, cosh de hyperbolische cosinusfunctie en "a" de schaalfactor.
Stap 2
Bekijk het effect van de schaalfactor op de vorm van de bovenleiding. Het kan worden gezien als de verhouding tussen de horizontale spanning in de kabel en het gewicht van de kabel per lengte-eenheid. Een kleinere schaalfactor resulteert dan in een diepere curve.
Stap 3
Bereken de bovenleidingfunctie met een alternatieve vergelijking. De vergelijking ‘y = a cosh (x / a)’ kan wiskundig worden bewezen als ‘y = a / 2 (e ^ (x / a) + e ^ (- x / a))’, waarin ‘e "is de basis van de natuurlijke logaritme en is ongeveer 2,71828.
Stap 4
Bereken de functie voor een elastische bovenleiding zoals "y = yo / (1 + et)", waarbij "yo" de aanvankelijke massa per lengte-eenheid is, "e" de veerconstante en "t" de tijd. Deze vergelijking beschrijft een stuiterende veer in plaats van een hangende kabel.
Stap 5
Bereken een echt voorbeeld van een bovenleiding. De functie "y = -127,7 cosh (x / 127,7) + 757,7" beschrijft de "St. Louis Arch" (Boog van St. Louis), de afmetingen zijn in voet.