Inhoud

Atomen in vaste stoffen zijn gerangschikt in een van de verschillende periodieke structuren die bekend staan als kristallen. Er zijn in totaal zeven kristallijne systemen. Voorbeelden zijn onder meer eenvoudig kubisch, volume-gecentreerd en face-gecentreerd. Het deel van het volume dat de atomen in een bepaald rooster hebben, staat bekend als de verpakkingsfactor. Het is mogelijk om deze factor van een materiaal, zoals diamant, te berekenen met enkele parameters van het materiaal en eenvoudige wiskunde.
Stap 1
Schrijf de vergelijking voor de verpakkingsfactor. De vergelijking is:
Verpakkingsfactor = Natomas x vacuüm / celcel
Aangezien "Nátomos" het aantal atomen in een eenheidscel is, is "Vátomo" het volume van het atoom en is "Vuntary cell" het volume van een eenheidscel.
Stap 2
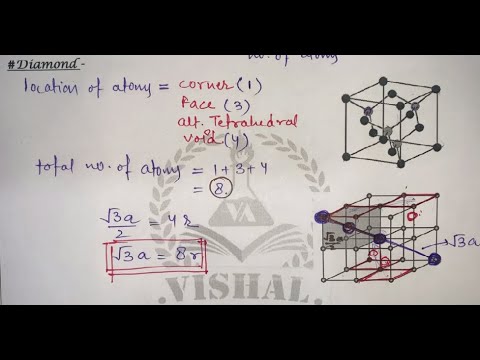
Vervang het aantal atomen per eenheidscel in de vergelijking. De diamant heeft acht atomen per eenheidscel, dus de formule is:
Verpakkingsfactor = 8 x vacuüm / celcel
Stap 3
Vervang het volume van het atoom in de vergelijking. Aangenomen dat ze bolvormig zijn, is het volume: V = 4/3 x pi x r³ De vergelijking voor de verpakkingsfactor ziet er nu uit als: Verpakkingsfactor = 8 x 4/3 x pi x r³ / Celcel
Stap 4
Vervang de waarde door het volume van de eenheidscel. Omdat de cel kubisch is, is het volume V-celcel = a³
De formule voor de pakkingsfactor wordt: Verpakkingsfactor = 8 x 4/3 x pi x r³ / a³ De straal van een atoom "r" is gelijk aan sqrt (3) x a / 8
De vergelijking wordt dus vereenvoudigd tot: sqrt (3) x pi / 16 = 0,3401