Hoe de eerste ionisatie-energie van het waterstofatoom gerelateerd aan de Balmer-serie te berekenen

Inhoud

• routebeschrijving

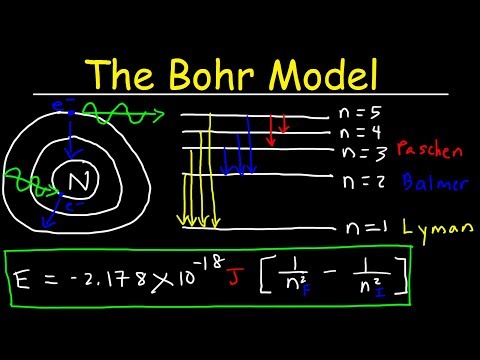
De Balmer-serie is de aanduiding voor de spectraallijnen van emissies van waterstofatomen. Deze spectraallijnen, die protonen zijn die worden uitgezonden in het zichtbare lichtspectrum, worden geproduceerd uit de energie die nodig is om een ​​elektron te verwijderen uit een atoom dat ioniserende energie wordt genoemd. Omdat het waterstofatoom slechts één elektron heeft, wordt de energie die nodig is om het te verwijderen de eerste ioniserende energie genoemd (maar in het geval van waterstof is er geen seconde). Het kan worden berekend via een reeks kleine stappen.

routebeschrijving

De Balmer-serie beschrijft de emissie van energie van verschillende atomen (Jupiterimages / Photos.com / Getty Images)

1. Bepaal de begin- en eindsenergietoestand van het atoom en vind het verschil van zijn inverse. Voor het eerste niveau van ionisatie is de uiteindelijke energietoestand oneindig, omdat het elektron wordt verwijderd van het atoom, zodat de inverse van dat getal 0 is. De initiële energietoestand is 1, de enige toestand waarin het waterstofatoom staat kan hebben, en de inverse van 1 is 1. Het verschil tussen 1 en 0 is 1.

2. Vermenigvuldig de Rydberg-constante (een getal dat belangrijk is in de atomaire theorie) met een waarde van 1.097 x 10 ^ (7) per meter (1 / m), door het verschil van de inverse van de energieniveaus, die in dit geval 1 is. geeft de oorspronkelijke waarde van de Rydberg-constante.

   
   

3. Bereken de inverse van het resultaat A, dat wil zeggen, deel het getal 1 door het resultaat van A. Dit geeft een waarde van 9,11 x 10 ^ (- 8) m; dit is de golflengte van de spectrale emissie.

4. Vermenigvuldig de constante van Planck met de snelheid van het licht en deel het resultaat door de emissiegolflengte. De Planck-constante vermenigvuldigen, die de waarde heeft van 6.626 x 10 ^ (-34) Joule maal tijden (J s) met de snelheid van het licht, die een waarde heeft van 3.00 x 10 ^ 8 meter per seconde (m / s) ), verkrijgen we 1,988 x 10 ^ (- 25) Joule keer meter (J m), en dit te delen door de golflengte (die gelijk is aan 9.11 x 10 ^ (-8) m), krijgen we 2.182 x 10 ^ (-18) J. Dit is de eerste ionisatie-energie van het waterstofatoom.

5. Vermenigvuldig de ionisatie-energie met Avogadro's aantal, wat zal resulteren in het aantal deeltjes in één mol van de stof. Het vermenigvuldigen van 2.182 x 10 ((-18) J met 6.022 x 10 ((23), resulteert in 1.312 x 106 Joule per mol (J / mol), of 1312 kJ / mol, wat is zoals gewoonlijk wordt geschreven in chemie.