
Inhoud
- Bepaal de tijd in de lucht.
- Stap 1
- Stap 2
- Stap 3
- Stap 4
- Bepaal de maximale hoogte
- Stap 1
- Stap 2
- Stap 3
- Bepaal de horizontale afgelegde afstand.
- Stap 1
- Stap 2
- Stap 3
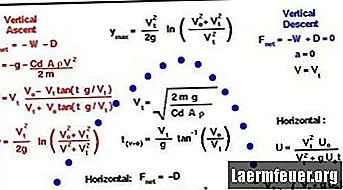
Hier is de methode voor het berekenen van het traject van een kogel en specifiek de tijd in de lucht, het bereik en het hoogste punt van zijn traject. In dit voorbeeld zijn enkele aannames gedaan om de berekening te vereenvoudigen: verwaarloosbare luchtweerstand, geen wind en onvoldoende schietafstand om de rotatie van de aarde te laten werken.
Bepaal de tijd in de lucht.
Stap 1
Eerst moet de vorm van de boog worden bepaald. Is de hoek aanvankelijk naar beneden, dan is het hoogste punt al bekend als de schietpositie. Zelfs een opwaartse hoek kan het doel als hoogste punt hebben, of deze hoek nu ondiep is of voldoende hoog (h). Dit kan worden bepaald in stap vier, wanneer de luchttijd wordt bepaald.
Stap 2
Als de hoek "?" De afvuursnelheid is die tussen het aanvankelijke traject van het projectiel en het horizontale vlak, dus de aanvankelijke verticale snelheid is V (i) = V.sen?.
Stap 3
De luchttijd wordt gevonden met behulp van de vergelijking van de positie h = V.sen? .T - (0,5) g.t ^ 2, waarbij g = 9,8 meter / seconden ^ 2. Alle variabelen zijn bekend, behalve de tijd in de lucht, t, dus dit kan worden opgelost met de kwadratische functie: ax ^ 2 + bx + c = 0, dus x = [-b ± √ (b ^ 2-4ac )] / 2a
Stap 4
Als meer dan één oplossing voor t is toegestaan, aangezien h> 0, dan komt het eerste resultaat overeen met wanneer hoogte = h op het klimpad en het tweede met wanneer hoogte = h op het afdalingspad. Als h <0, dan was de enige echte oplossing voor t toegestaan, en de andere is negatief.
Bepaal de maximale hoogte
Stap 1
Als? <0, dan is al bekend dat de maximale hoogte de beginhoogte is, h = 0.
Stap 2
Als er meer dan één keer was, t, waarin de kogel h uitstrekt, dan komt de kleinste t overeen met een vliegroute waarbij h het hoogste punt is. De hoogste t komt overeen met de kogel die een hogere hoogte bereikt voordat hij terugkeert naar h, om deze hoogte op te lossen, gebruikt u de formule V (t) = V (0) - 9,8t om de waarde van t te vinden wanneer de verticale snelheid is nul. Met andere woorden, voor welke tijd, t, V.sen? = 9,8t.?
Stap 3
Door t op te lossen en de hoogte-formule te verbinden, hebben we de maximale hoogte: hm = V.sen? - 4,9t ^ 2. Dezelfde benadering wordt gebruikt voor een maximale hoogte-oplossing, als er maar één oplossing voor t was toegestaan.
Bepaal de horizontale afgelegde afstand.
Stap 1
Om de horizontale afstand te bepalen die is afgelegd tegen de tijd dat de kogel hoogte h bereikt, moet u eerst de aanvankelijke horizontale snelheid van de kogel berekenen: v (i) = V.cos (?).
Stap 2
Vervang de tijd, t, wanneer de kogel de uiteindelijke hoogte bereikt, A, in de positie van de formule met horizontale snelheid: A = V.cosΘ.t. Ervan uitgaande dat er geen luchtweerstand en geen acceleratieterm aan de rechterkant is.
Stap 3
Als er meer dan één keer t was toen de hoogte in h was, dan zijn de twee posities van "A" geldig, waarbij het hoogste punt hm is voor de kleinste van de twee "A". De horizontale en verticale eindposities en het bereikte hoogste punt zijn nu bekend en bepalen daarmee het traject van de kogel.